Sono qui, continuando da qui.
Applicazione alle funzioni
As a general rule, functions should already be written with matrix arguments in mind and should consider whole matrix operations in a vectorized manner. Sometimes, writing functions in this way appears difficult or impossible for various reasons. For those situations, Octave provides facilities for applying a function to each element of an array, cell, or struct.
Function File: arrayfun (func, A)
Function File: x = arrayfun (func, A)
Function File: x = arrayfun (func, A, b, ...)
Function File: [x, y, ...] = arrayfun (func, A, ...)
Function File: arrayfun (..., "UniformOutput", val)
Function File: arrayfun (..., "ErrorHandler", errfunc)
Execute a function on each element of an array.
This is useful for functions that do not accept array arguments. If the function does accept array arguments it is better to call the function directly.
The first input argument func can be a string, a function handle, an inline function, or an anonymous function. The input argument A can be a logic array, a numeric array, a string array, a structure array, or a cell array. By a call of the function arrayfun all elements of A are passed on to the named function func individually.
The named function can also take more than two input arguments, with the input arguments given as third input argument b, fourth input argument c, ... If given more than one array input argument then all input arguments must have the same sizes, for example:

If the parameter val after a further string input argument "UniformOutput" is set true (the default), then the named function func must return a single element which then will be concatenated into the return value and is of type matrix. Otherwise, if that parameter is set to false, then the outputs are concatenated in a cell array. For example:
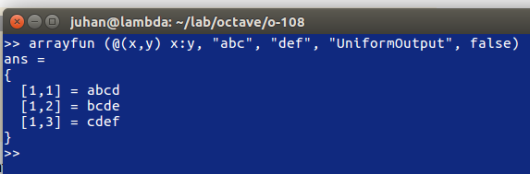
If more than one output arguments are given then the named function must return the number of return values that also are expected, for example:

If the parameter errfunc after a further string input argument "ErrorHandler" is another string, a function handle, an inline function, or an anonymous function, then errfunc defines a function to call in the case that func generates an error. The definition of the function must be of the form function [...] = errfunc (s, ...) where there is an additional input argument to errfunc relative to func, given by s. This is a structure with the elements "identifier", "message", and "index" giving, respectively, the error identifier, the error message, and the index of the array elements that caused the error. The size of the output argument of errfunc must have the same size as the output argument of func, otherwise a real error is thrown. For example:

Function File: y = spfun (f, S)
Compute f(S) for the nonzero values of S.
This results in a sparse matrix with the same structure as S. The function f can be passed as a string, a function handle, or an inline function.

per contro

Built-in Function: cellfun (name, C)
Built-in Function: cellfun ("size", C, k)
Built-in Function: cellfun ("isclass", C, class)
Built-in Function: cellfun (func, C)
Built-in Function: cellfun (func, C, D)
Built-in Function: [a, ...] = cellfun (...)
Built-in Function: cellfun (..., "ErrorHandler", errfunc)
Built-in Function: cellfun (..., "UniformOutput", val)
Evaluate the function named name on the elements of the cell array C.
Elements in C are passed on to the named function individually. The function name can be one of the functions
isempty Return 1 for empty elements.islogical Return 1 for logical elements.isnumeric Return 1 for numeric elements.isreal Return 1 for real elements.length Return a vector of the lengths of cell elements.ndims Return the number of dimensions of each element.numel, prodofsize Return the number of elements contained within each cell element. The number is the product of the dimensions of the object at each cell element.size Return the size along the k-th dimension.isclass Return 1 for elements of class.
Additionally, cellfun accepts an arbitrary function func in the form of an inline function, function handle, or the name of a function (in a character string). The function can take one or more arguments, with the inputs arguments given by C, D, etc. Equally the function can return one or more output arguments. For example:

The number of output arguments of cellfun matches the number of output arguments of the function. The outputs of the function will be collected into the output arguments of cellfun like this:

Note that per default the output argument(s) are arrays of the same size as the input arguments. Input arguments that are singleton (1x1) cells will be automatically expanded to the size of the other arguments.
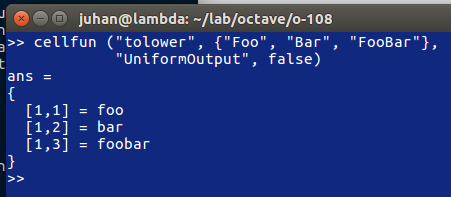
If the parameter "UniformOutput" is set to true (the default), then the function must return scalars which will be concatenated into the return array(s). If "UniformOutput" is false, the outputs are concatenated into a cell array (or cell arrays). For example:
Given the parameter "ErrorHandler", then errfunc defines a function to call in case func generates an error. The form of the function is function [...] = errfunc (s, ...) where there is an additional input argument to errfunc relative to func, given by s. This is a structure with the elements "identifier", "message" and "index", giving respectively the error identifier, the error message, and the index into the input arguments of the element that caused the error. For example:

Use cellfun intelligently. The cellfun function is a useful tool for avoiding loops. It is often used with anonymous function handles; however, calling an anonymous function involves an overhead quite comparable to the overhead of an m-file function. Passing a handle to a built-in function is faster, because the interpreter is not involved in the internal loop. For example:
a = {...}
v = cellfun (@(x) det (x), a); # compute determinants
v = cellfun (@det, a); # faster
Function File: structfun (func, S)
Function File: [A, ...] = structfun (...)
Function File: structfun (..., "ErrorHandler", errfunc)
Function File: structfun (..., "UniformOutput", val)
Evaluate the function named name on the fields of the structure S. The fields of S are passed to the function func individually.
structfun accepts an arbitrary function func in the form of an inline function, function handle, or the name of a function (in a character string). In the case of a character string argument, the function must accept a single argument named x, and it must return a string value. If the function returns more than one argument, they are returned as separate output variables.
If the parameter "UniformOutput" is set to true (the default), then the function must return a single element which will be concatenated into the return value. If "UniformOutput" is false, the outputs are placed into a structure with the same fieldnames as the input structure.

Given the parameter "ErrorHandler", errfunc defines a function to call in case func generates an error. The form of the function is function [...] = errfunc (se, ...) where there is an additional input argument to errfunc relative to func, given by se. This is a structure with the elements "identifier", "message" and "index", giving respectively the error identifier, the error message, and the index into the input arguments of the element that caused the error. For an example on how to use an error handler, see cellfun.
Consistent with earlier advice, seek to use Octave built-in functions whenever possible for the best performance. This advice applies especially to the four functions above. For example, when adding two arrays together element-by-element one could use a handle to the built-in addition function @plus or define an anonymous function @(x,y) x + y. But, the anonymous function is 60% slower than the first method. See Operator Overloading, for a list of basic functions which might be used in place of anonymous ones.